Skip to contents

Stratigraphic Paleobiology for Phenotypic Evolution

Source: vignettes/phenotypic_evolution.Rmd
phenotypic_evolution.Rmd

Introduction

Here we describe the modeling pipeline for the stratigraphic paleobiology of phenotypic evolution. For details how this can be combined with the paleoTS package (Hunt 2006), see

vignette("paleoTS_functionality")

First, let’s load all required packages:

Modes of evolution in the time domain

Implemented modes of evolution

The StratPal package provides three functions for simulating different modes of evolution in the time domain:

  • stasis simulates evolutionary stasis as independent, normally distributed random variables with mean mean and standard deviation sd (Hunt 2006).

  • random_walk simulates trait evolution following a (potentially biased) random walk with variability sigma, directionality mu, and initial trait value y0 (e.g. Bookstein 1987). Setting mu to a negative (positive) value will make the value of the random walk decrease (increase) over time, sigma determines the effect of randomness on the trait values.

  • ornstein_uhlenbeck corresponds to convergence to a phenotypic optimum, where mu is the optimal value (long term mean), theta determines how fast mu is approached, sigma the noise level, and y0 the initial trait value (Lande 1976).

Use vignette("advanced_functionality") for guidelines to implement your own modes of evolution.

Visualization

You can visualize the different modes of evolution using the following pipeline:

seq(0, 1, by = 0.01) |>             # times of simulation in Myr. Simulate over 1 Myr years with 10 kyr resolution
  random_walk(sigma = 1, mu = 3) |> # simulate random walk with increasing trait values
  plot(type = "l",                  # plot results
       xlab = "Time [Myr]",
       ylab = "Trait value")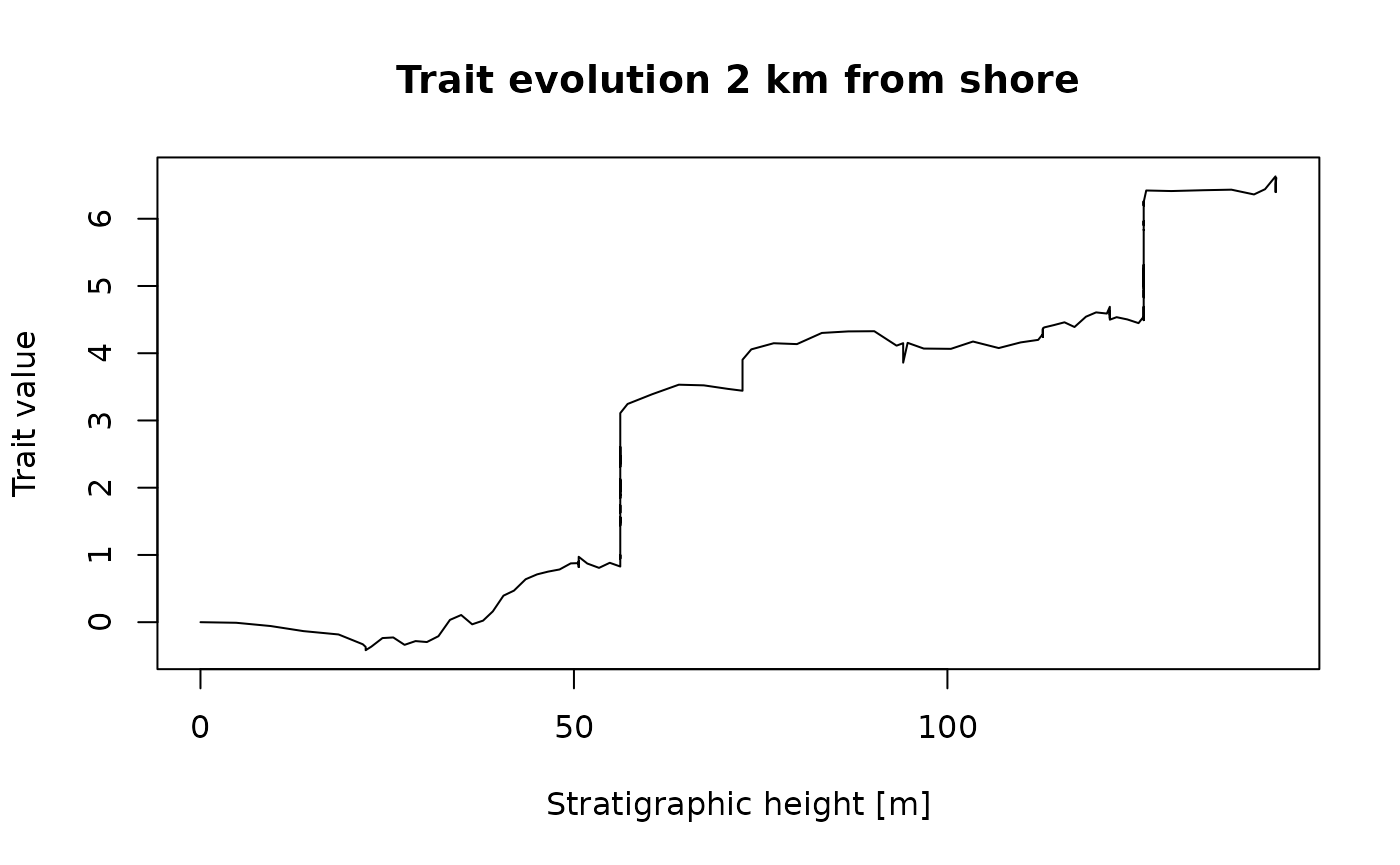

plot of a random walk

Task: Modify the pipeline to get an intuition for the different modes of evolution. What are the effects of their parameters, and what is their biological meaning?

Stratigraphic domain

We are interested in how phenotypic evolution is preserved in the stratigraphic record, i.e. how trait evolution within a lineage is preserved at a specific location in the stratigraphic record. Here we develop the modeling pipelines to answer this question.

Age-depth models

As an example, we compare the preservation of trait evolution 2 km and 12 km offshore in the carbonate platform in scenario A from Hohmann et al. (2024). See ?scenarioA and vignette("StratPal") for details on scenario A.

First define the age-depth models:

adm_2km = tp_to_adm(t = scenarioA$t_myr,    # 2 km from shore
                h = scenarioA$h_m[,"2km"],
                T_unit = "Myr",
                L_unit = "m")

adm_12km = tp_to_adm(t = scenarioA$t_myr,   # 12 km from shore
                h = scenarioA$h_m[,"12km"],
                T_unit = "Myr",
                L_unit = "m")

plot(adm_2km,       # plot age-depth model 2 km from shore
     lwd_acc = 2,   # plot thicker lines for intervals with sediment accumulation (lwd = line width)
     lty_destr = 0) # don't plot destructive intervals/gaps (lty = line type)
T_axis_lab()        # add time axis label
L_axis_lab()        # add length axis label
title("Age-depth model 2 km from shore")

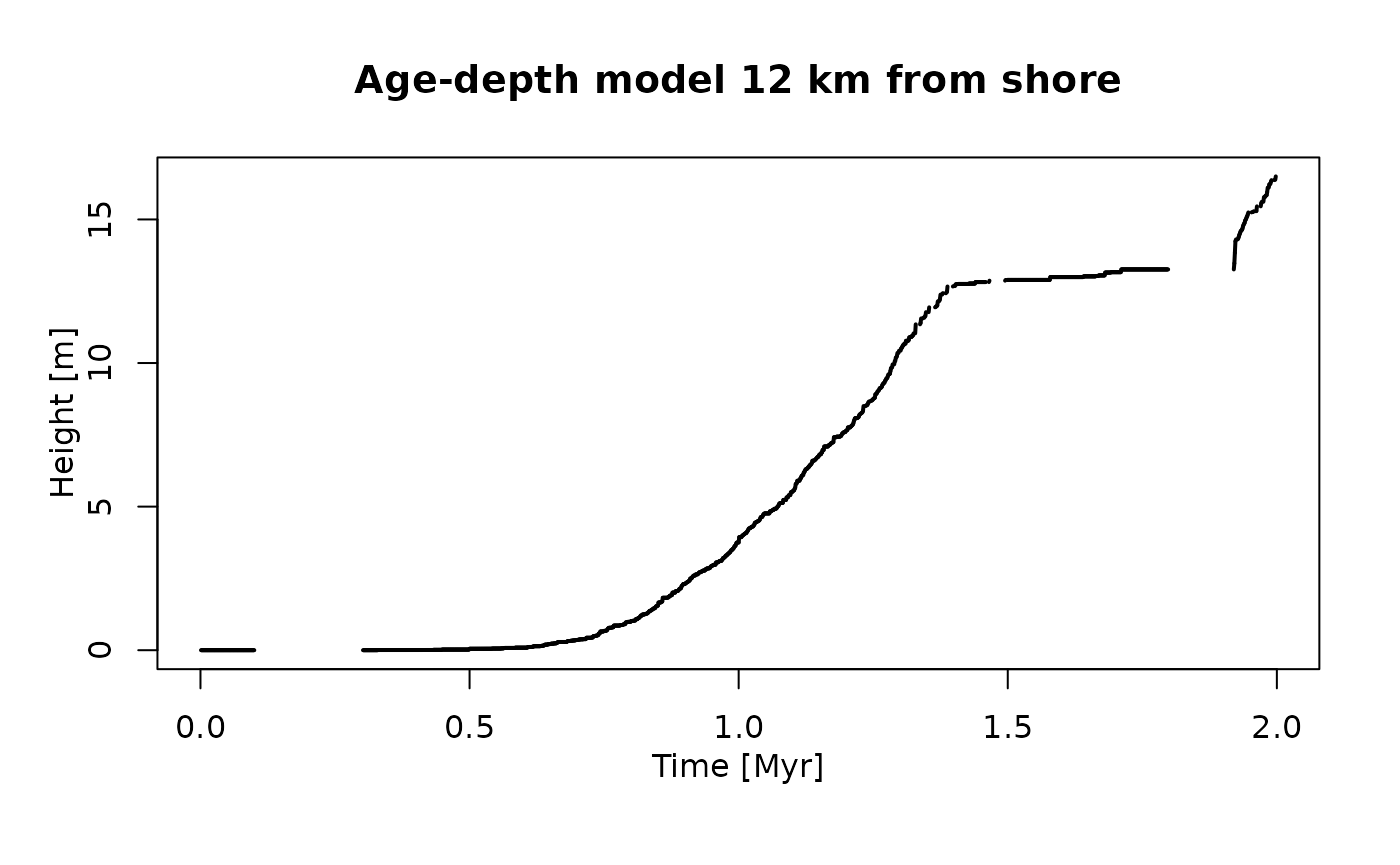
plot(adm_12km,      # plot age-depth model 12 km from shore
     lwd_acc = 2,   
     lty_destr = 0) 
T_axis_lab() 
L_axis_lab() 
title("Age-depth model 12 km from shore")

2 plots of age-depth models, one 2 km from shore and one 12 km from shore2 plots of age-depth models, one 2 km from shore and one 12 km from shore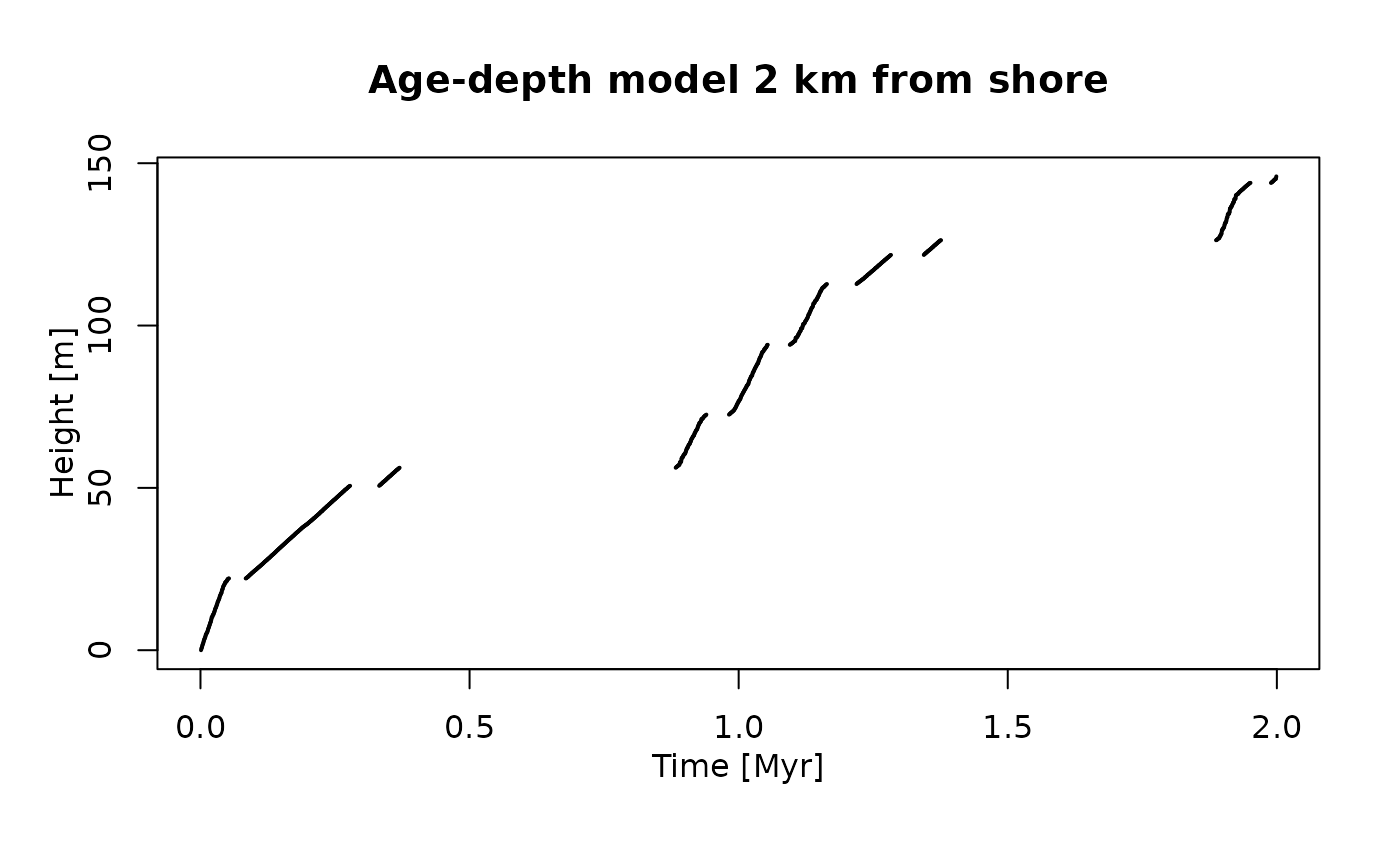

Stratigraphic expression of phenotypic evolution

We use the defined age-depth models to transform the simulated trait values from the time domain into the depth domain via time_to_strat:


seq(from = min_time(adm_2km), to = max_time(adm_2km), by = 0.01) |> # sample every 10 kyr over the interval covered by the adm 
  random_walk(sigma = 1, mu = 3) |>                                 # simulate random walk
  time_to_strat(adm_2km, destructive = FALSE) |>                    # transform data from time to strat domain
  plot(type = "l",                                                  # plot
       orientation = "lr",
       xlab = paste0("Stratigraphic height [", get_L_unit(adm_2km), "]"),
       ylab = "Trait value",
       main = "Trait evolution 2 km from shore")

plot of the stratigraphic experssion of a random walk 2 km from shore.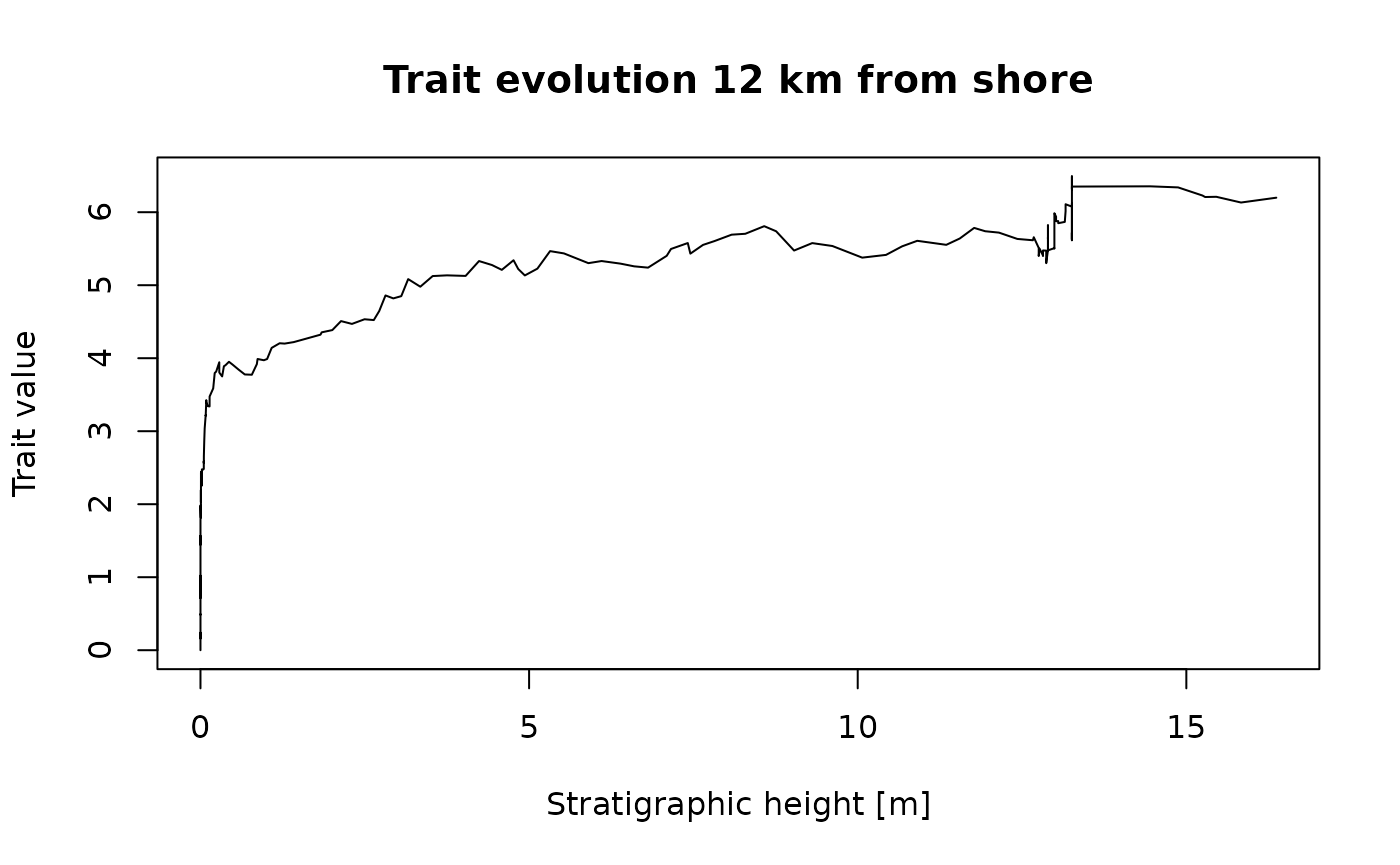

This is what a biased random walk in the time domain would look like if it was observed 2 km offshore in the simulated carbonate platform. The large jumps in traits correspond to long hiatuses caused by prolonged drops in relative sea level (Hohmann et al. 2024). Compare this figure to the random walk in the time domain (without stratigraphic distortions).

12 km offshore, the preservation is very different:

seq(from = min_time(adm_12km), to = max_time(adm_12km), by = 0.01) |> # sample every 10 kyr over the interval covered by the adm 
  random_walk(sigma = 1, mu = 3) |>                                   # simulate random walk
  time_to_strat(adm_12km, destructive = FALSE) |>                     # transform data from time to strat domain
  plot(type = "l",                                                    # plot results
       orientation = "lr",
       xlab = paste0("Stratigraphic height [", get_L_unit(adm_12km), "]"),
       ylab = "Trait value",
       main = "Trait evolution 12 km from shore")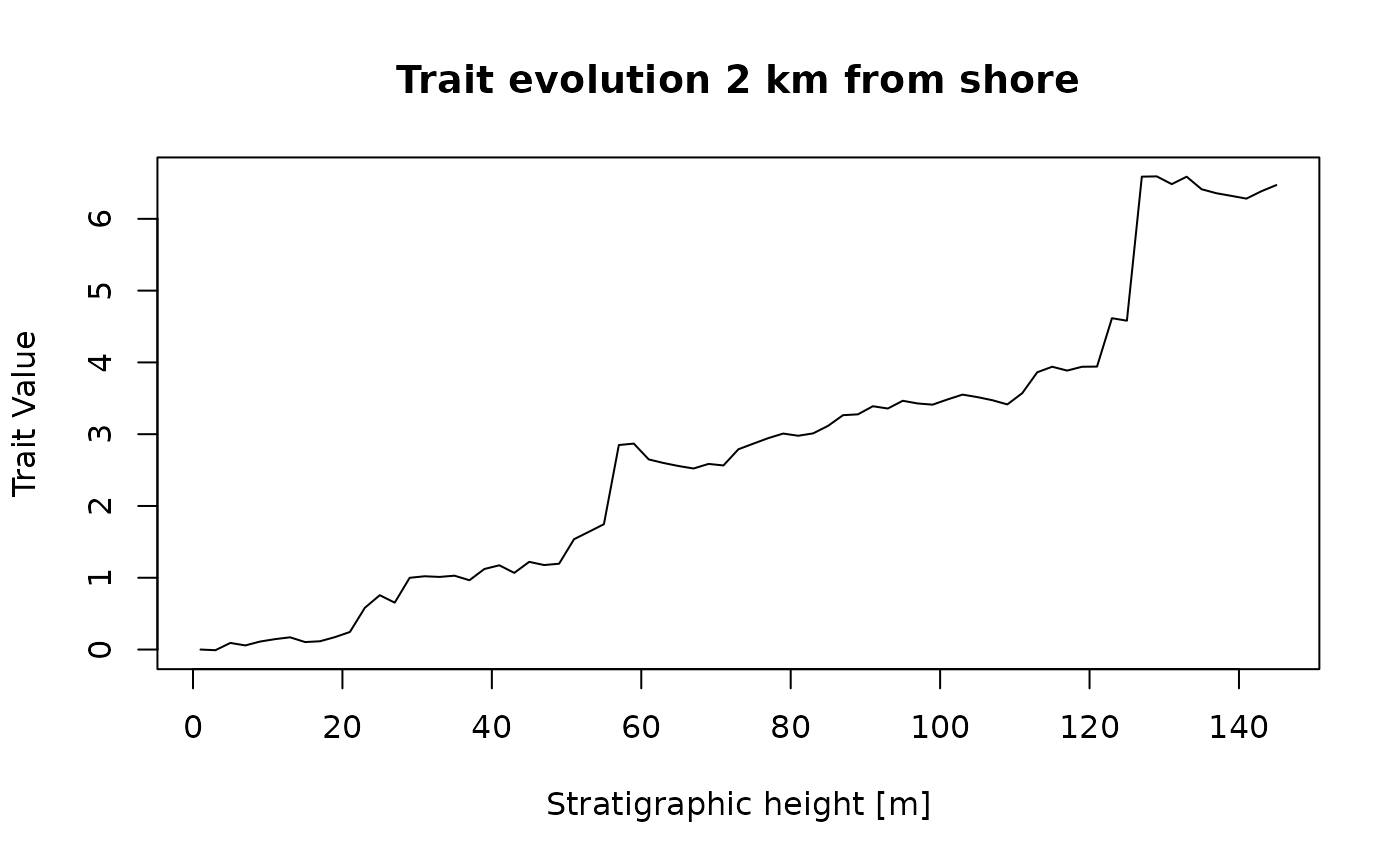

plot of the stratigraphic expression of a random walk 12 km from shore.

You can also see two jumps, but the first is at a different location compared to the section 2 km offshore. Looking at the age-depth models, we can see why this is: 2 km offshore, the jumps are caused by prolonged hiatuses that are associated with the massive drops in sea level around 0.5 Myr and 1.5 Myr. 12 km offshore, the age-depth model shows fewer gaps, but prolonged intervals with low sedimentation rates at the beginning of the simulation and at around 1.5 Myr. This leads to intervals where the rate phenotypic evolution appears to be accelerated because of (sedimentological) condensation (Hohmann 2021). You can see that not all artefactual jumps in traits observable in the stratigraphic record are caused by gaps.

Task: How does this effect vary between different modes of evolution (with different parameter choices), and at different locations in the platform (e.g., along an onshore-offshore gradient)? Can you make any general statements about where you see the strongest effects?

Prescribing a sampling strategy

The above plots already give us a good idea of how stratigraphic effects can change our interpretation of trait evolution.

However, there is a small imperfection. Because we simulate the lineage every 10 kyr, it is sampled irregularly in the stratigraphic domain: If sedimentation rates are high, samples can be multiple meters apart, but if sedimentation rates are low, they are only a few centimeters apart.

To fix this, we want to prescribe where in the stratigraphic domain samples are taken. This allows us to examine the effect that different sampling strategies have on our perception of trait evolution. We do this in the following steps:

  1. Determine sampling locations in the stratigraphic domain.
  2. Calculate what times correspond to said sampling locations via strat_to_time.
  3. Simulate a lineage at said times.
  4. Transform the simulated trait values back into the stratigraphic domain using time_to_strat.
  5. Plot the result.

Let’s assume we take a sample every 2 meters. Then our five steps above result in the following modeling pipeline:

dist_between_samples_m = 2
sampling_loc_m = seq(from = 0.5 * dist_between_samples_m,
                     to = max_height(adm_2km),
                     by = dist_between_samples_m)

sampling_loc_m |>                                  # sampling locations
  strat_to_time(adm_2km) |>                        # determine times where lineage is sampled
  random_walk(sigma = 1, mu = 3) |>                # simulate trait values at these times
  time_to_strat(adm_2km, destructive = FALSE) |>   # transform trait values to stratigraphic domain
  plot(orientation = "lr",                         # plot stratigraphic data
       type = "l",        
       ylab = "Trait Value",
       xlab = paste0("Stratigraphic height [", get_L_unit(adm_2km), "]"),
       main = "Trait evolution 2 km from shore")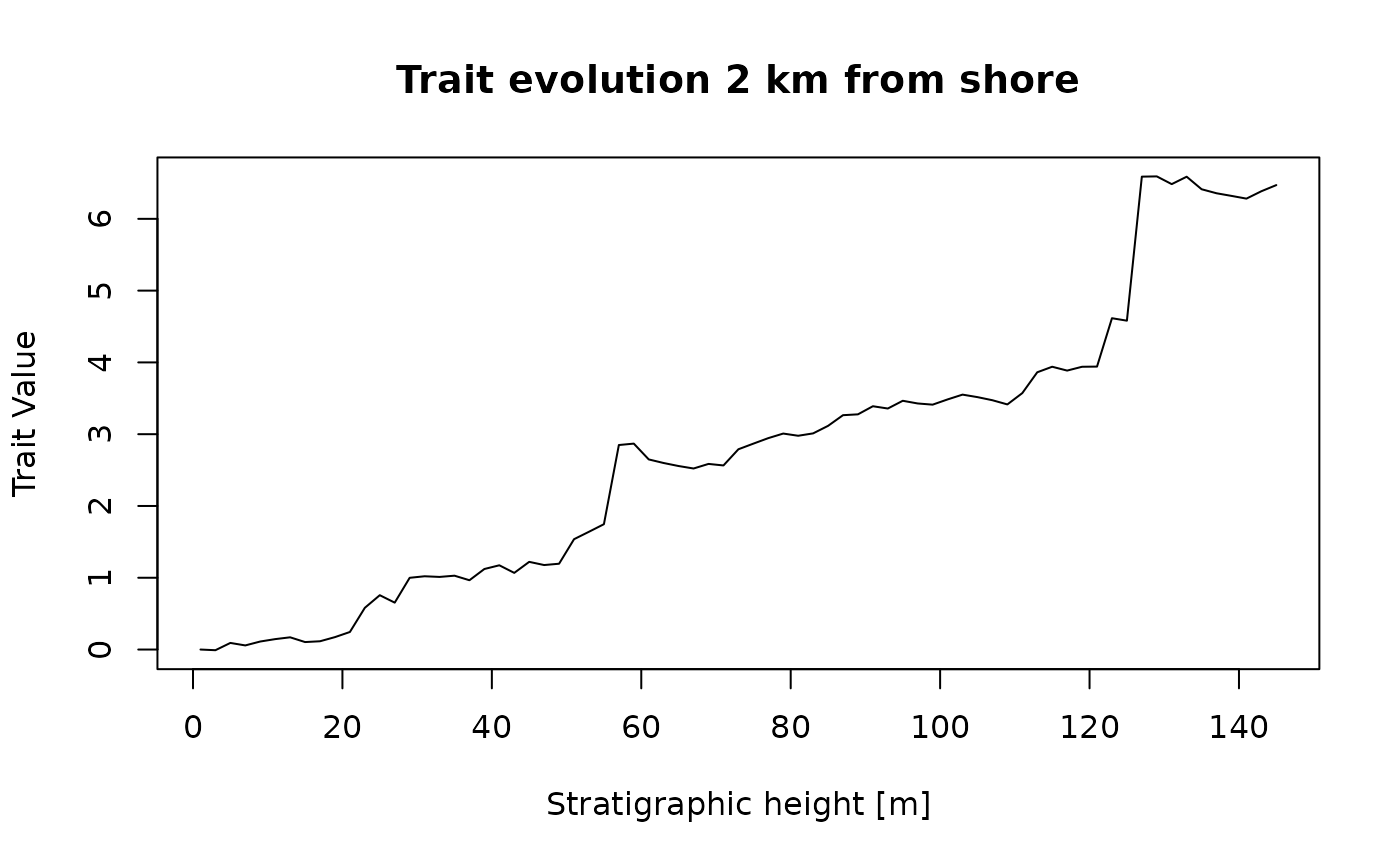

plot of the stratigraphic expression of a random walk 2 km from shore, sampled every 2 km.

There we have it! This is what the lineage would look like if it was sampled every 2 meters in a sections 2 km from shore.

Task: How does prescribing a sampling strategy change the interpretations of your last task? Can you draw any conclusions about which sampling strategy is best suited for a given environment or mode of evolution?

Further reading

For details on how the StratPal package (Hunt 2006) can be integrated with the paleoTS package, see

vignette("paleoTS_functionality")

Run

vignette("event_data")

for details on how to model stratigraphic paleobiology of event data such as individual fossils and first/last occurrences of taxa, or explore the vignette online under mindthegap-erc.github.io/StratPal/articles/event_data.

See also

vignette("advanced_functionality")

for details on how to expand on the modeling pipelines described here, or explore the vignette online under mindthegap-erc.github.io/StratPal/articles/advanced_functionality.

References