Quantifying stratigraphic order

library(stratcols)

Introduction

This vignette describes how to quantify stratigraphic order.

Setup

First, we define a stratigraphic column:

s = as_stratcol(thickness = runif(90), # random bed thicknesses
                facies = rep(c(1,2,3), 30)) # repeat facies 1, 2 and 3 
plot(s)

Estimating Markov metrics

We can then estimate the transition matrix between facies using

m = transition_matrix(s)
m
#>    from
#> to  1 2 3
#>   1 0 0 1
#>   2 1 0 0
#>   3 0 1 0
#> attr(,"class")
#> [1] "fa_tran_mat_p"

and estimate the markov order metric (MOM) from it using

get_mom(m)
#> [1] 1

Estimating run metrics

The run order metrics (ROM) can be estimated using

rom_observed = get_rom(s)
rom_observed
#> [1] 1.41573

To put this value into context, we randomize the section to estimate the distribution of rom values

n = 10000
rom_vals = rep(NA, n)
for (i in seq_len(n)){
  randomized_column = shuffle_col(s)
  rom_vals[i] = get_rom(randomized_column)
}

hist(rom_vals,
     main = "distribution of ROM values")
lines(x = rep(rom_observed, 2), y = c(0,n), col = "red")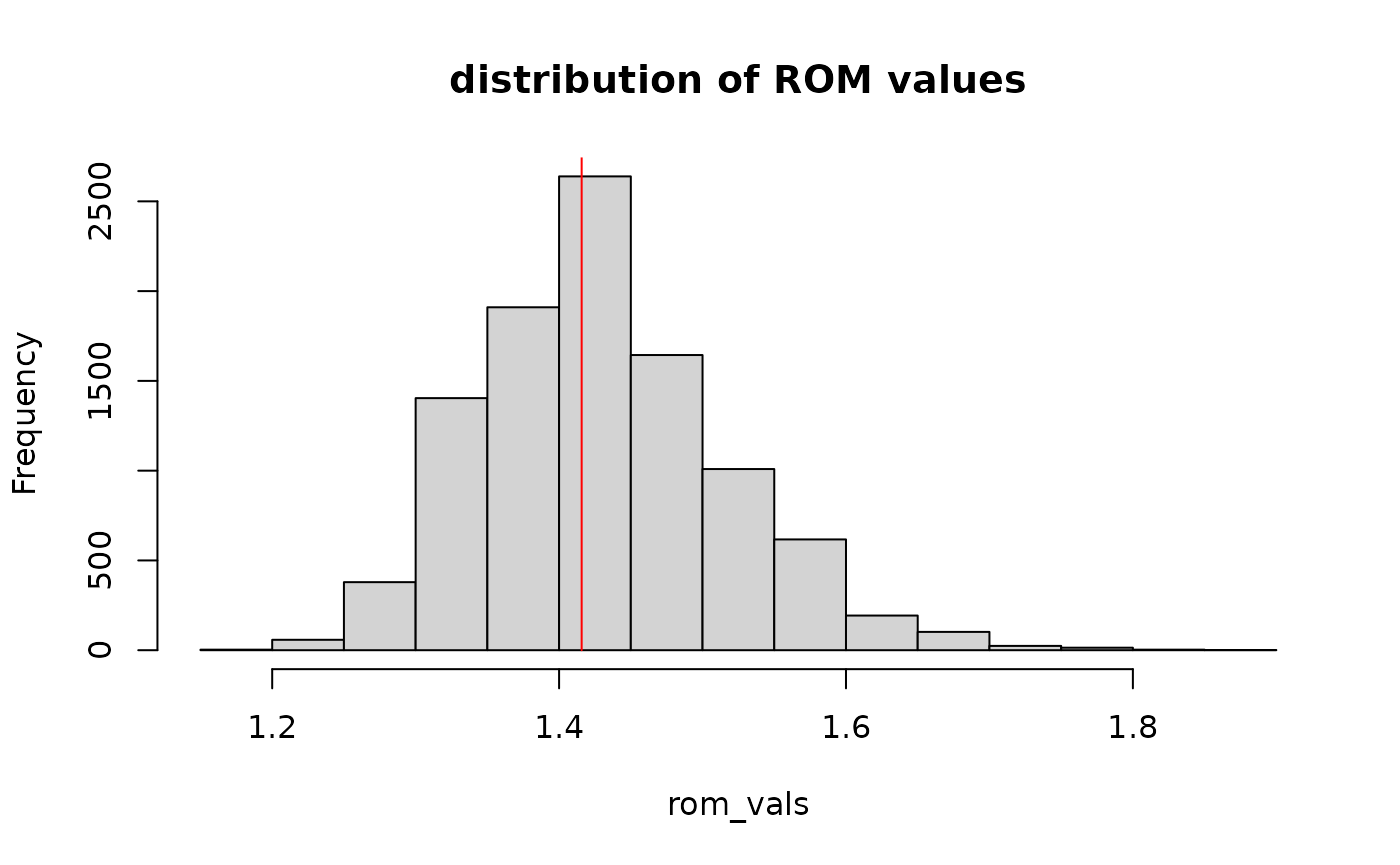

Here the red line indicates how extreme the rom value of the stratigraphic column s is compared to the expected distribution of rom values based on random reordering of the beds.

Estimating Markov Order Metrics

To estimate markov order metrics, some data preparation is needed to make sure all assumptions on the encoding of the stratigraphic column are met. Let’s start by defining an example stratigraphic column:

set.seed(1)
s = as_stratcol(thickness = runif(30), fa = rep(c(1,2,3), 10)) # uniform bed thickness, ordered facies
s = shuffle_col(s, allow_rep = TRUE) # randomize order of beds, allowing  for repetitions
plot(s)

Check for successive beds with identical facies

MOM only examines transitions between facies, and ignores beds with identical facies. To meet this criterion, we first need to merge all beds with identical facies:

s_merged = merge_beds(s, mode = "identical facies")
plot(s_merged)

### Rearrange facies names

The next assumption is that facies are enumerated using integers based on their order of appearance in the column. We can do this using order_facies_names:

s_ord_names = order_facies_names(s_merged)
plot(s_ord_names)

### estimating the transition matrix

Now we can estimate the facies transition matrix:

m = transition_matrix(s_ord_names)
m
#>    from
#> to          1         2         3
#>   1 0.0000000 0.8333333 0.1666667
#>   2 0.1428571 0.0000000 0.8571429
#>   3 0.7142857 0.2857143 0.0000000
#> attr(,"class")
#> [1] "fa_tran_mat_p"

Note that because we have merged beds with identical facies, entries on the diagonal are 0 - facies do not transition into themselves.

Estimating MOM

From the facies transition matrix, MOM can be estimated via

get_mom(m)
#> [1] 0.6031746

A MOM value of 0 indicates unordered facies, a value of 1 reflects perfect order and deterministic transitions between facies.

Further reading

See also

vignette("stratcols_doc")

for a description of the classes used in the package and a description of the larger scale structure.